Maître Erwin

L'un des secrets de la rosace dessinée par Maître Erwin (pour la cathédrale de Strasbourg)

Concernerai peut être l'un des secret de l'univers (sa géométrie)

Erwin von Steinbach (1244-1318)https://fr.wikipedia.org/wiki/Erwin_von_Steinbach
pour la facade dont la grande rose de la cathédrale de Strasbourg https://fr.wikipedia.org/wiki/Cath%C3%A9drale_Notre-Dame_de_Strasbourg
La Rosace de Maître Erwin

Et ce secret est plus géométrique qu'artistique ou ésotérique: 

Comparons d'abord cette rosace avec cette image là   

et qui represente l'une des quatre familles de courbes que l'on peut definir sur un tore 

comme on peut le voir dans les six images ci-dessous 
 
 
 
 
 

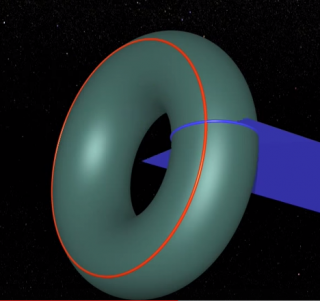
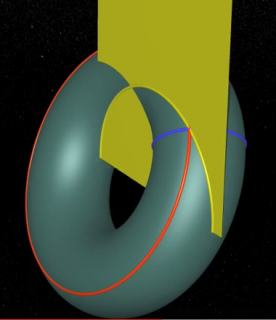
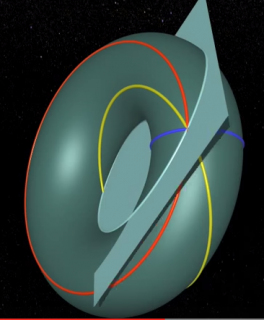
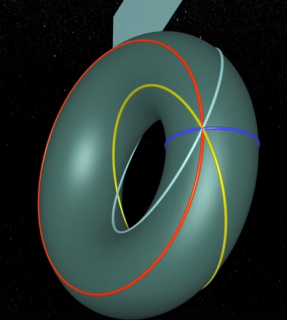
Un tore est constitué de quatre familles de cercles (sur l'image cercles de couleurs bleu (foncé) , rouge , jaune et blanc (ou bleu ciel selon l'image)
deux cercles appartenants à une même famille ne se rencontrent pas

un cercle bleu (foncé) rencontre un cercle rouge en un seul point
un cercle jaune et un cercle blanc se rencontrent en deux points
(ces deux familles de cercles sont nommés cercles de Villarceau (1813–1883) https://fr.wikipedia.org/wiki/Cercles_de_Villarceau
 
en ce qui concerne les cercles jaunes, ceux-ci sont nommés cercles de Hopf (1894-1971)https://fr.wikipedia.org/wiki/Fibration_de_Hopf

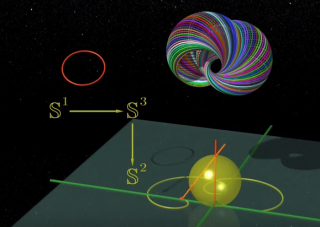
pour comprendre plus précisement en quoi l'image initiale est en rapport avec le propos on imagine ici 
ci-dessous 
 
 
 
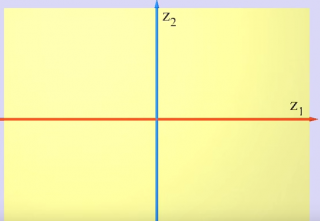
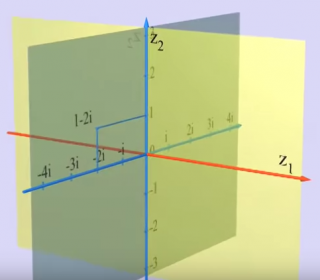
on imagine un espace de dimension 4 représenté par deux droites de l'espace à 4 dimension Z1 et Z2
chacune de ces droites appartenants à un plan complexe 
contrairement à ce que l'on peut voir dans les images ci-dessous il n'est pas possible de voir les deux plans simultanéments
cette image qui donne une représentation tridimentionnelle de ces deux plans ont l'air de se couper sur une droite 
mais dans l'espace quadridimentionnel les deux plans se coupent sur un point (le point origine des quatres axes )

ici ci-dessous le "cercle" (on dira de rayon 1 -unité-) represente en fait une hyper-sphère de dimension 3 plongée dans l'espace à 4 dimensions
 
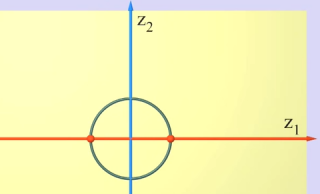
l'ensemble des points sur cette hyper-sphere sont l'ensemble des points dans l'espace à 4 dimensions qui sont situés à la distance unité de l'origine
dans l'image ci-dessous on "voit" comment cette hyper-sphere rencontre le premier axe definit par Z1
 
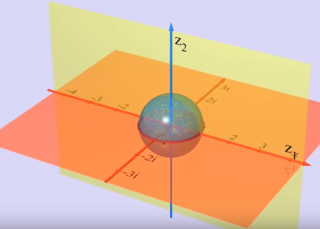
c'est à dire que cette rencontre est un cercle (rouge dans l'image) mais est une sphere (classique) c'est à dire une hypersphere de dimension 2 (qui pourrait être plongée dans l'espace à 3 dimensions)
mais ici elle est plongée dans l'espace à 4 dimensions ( elle en reste pas moins une sphere classique)
là dans l'image ci-dessous on "voit" comment cette hyper-sphere rencontre le deuxieme axe definit par Z2
 
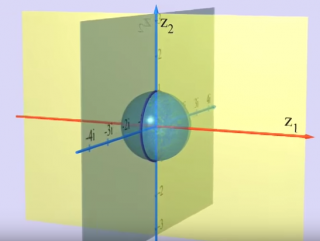
en fait pour toute droite formant un plan complexe 
là par exemple dans l'image cidessous on voit un autre cercle (donc une sphere classique)
 
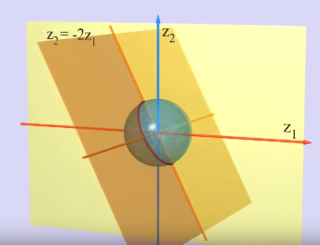
dans l'image ci dessous on voit que la projection stéréoscopique d'un point de la sphere classique (la sphere en jaune dans l'image -dite sphere S2 puisque sa surface est de dimension 2) correspond un point sur un plan complexe
ce point couplé au point correspondant sur cette sphere (les deux points representés par les petites boules rouges) definissent un segment de droite
chacune de ces droites se comportant celle de l'image précedente à laquelle correspond un cercle dit S1 -puisque on peut aussi dire qu'un cercle est une sphere dont la surface est de dimension 1 (rouge dans l'image)   
l'ensemble de tous ces cercles forme la sphere de dimension 4 dit S3 comme on l'a vue dans les deux images précedentes
 

Hello Hilbertien,

J'ai pensé a toi en regardant cette vidéo, regarde a partir de 18 min !!

Bon calcul :-)

https://www.youtube.com/watch?v=2zJbenv5_Kc

merci Nossolar  

oui c'est effectivement très très très bizarre   

Salut,  



Question peut-être stupide et même surement, bah je tente:

Les faces des Pyramide n'auraient-elles pas les propriétés d'un triangle 2D rapporté en 4D vue de dessus?

La trigonométrie est la science du triangle

ABCD = x; y; z; z' et le point d'origine serait l'axe vertical à l'aplomb de la pyramide passant par intersection des diagonales:
Soi O = axe vertical qui lui est 1D passant par le sommet du pyramidion?

Mais c'est certainement une illusion de mon petit esprit pas très au point avec les mathématiques!

Je te fais confiance Hilbert Einstein.  

Je suis que dalle!     Christophoros  

(bon sinon là je vois pas trop , j'ai beaucoup de travail à faire et bon je suis paumé sur ta question )

moi franchement je suis un grand ignorant (j'aime Hilbert mais je suis pas Hilbert-loin de là, et si je suis Hilbertien, j'en suis pas pour autant digne de l'être)

ça m'a vachement hyper impressionné ce que dit Nossolar (son lien à la 18 minute environ)

ça je suis soufflé

Pas grave hilbertien, pour Albert c'était juste une sympathique et amicale boutade.
D’ailleurs tu veux rire: Je n'ai fait le rapprochement que ce soir!  

Non ce que j'essayais (si c'est juste) de te montrer, c'est qu'une pyramide 4 faces 2D vue de dessus est pour moi le parfait exemple d'un schéma 4D.
D’ailleurs relis le si tu as la forme je me suis corrigé le point d'origine n'est pas le sommet du pyramidion mais l'axe tout entier passant par le pyramidion (enfin je crois!
Pour le lien de Nosso j'ai pas encore regardé mais je vais le faire!
Merci de m'avoir répondu

je sais pas  Christophoros

bon en tout cas le lien de Nossolar là 18 minutes et cette histoire de sinus cosinus 

tu devrai voir ça 

c'est vachement chelou

franchement merci à lui !!

Merci à vous deux. Oui! époustouflant!

Quand je dis qu'il ne faut rejeter aucune religion mais qu'au contraire il faut y chercher "les traits d'union", pour pouvoir dans le futur assemblé "la vérité"!

Les Hébreux disent qu'à la base nous sommes tous "les mêmes", un seul et même peuple comme avant Babel!
La seule différence entre eux et nous c'est qu'ils sont élus mais élus par qui et pour quoi faire?
Ils pensent que par le passé quand nous nous sommes densifié dans la matière nous avons perdu "le regard (la connexion) de dieu".
A ce moment là les humains se seraient scindés en deux groupes: l'Orient aurait choisi la soumission tandis que l'occident préféra se cacher du regard de Dieu.
La peur et la détresse fit consensus parmi les humains et là où ce n'est pas clair pour moi "ou les hommes ou Dieu" auraient effectué un prélèvement de personnes qui ont étés élues (d'où le terme élus) dans les deux groupes "je me répète soit par la volonté des hommes soit par celle de Dieu" afin de former les tribus d'Israël.
Leur mission?
Faire retrouver la communication (vidéo, son) entre les hommes et leur créateur.

Elle est super cette vidéo! "Encore merci à vous deux...

Christophoros encore mieux que ce que je pensais tout à l'heure  

(oui vraiment vraiment merci Nossolar car là il y a une belle demo à faire , franchement là ça m'interresse cette démo car d'un transcendant la fonction donne un algebrique irrationnel)

cela viens de l'égalité exprimée en radian de 

...donc Nossolar et Christophoros (encore merci à vous pour avoir fait remarquer plusieurs choses)

et à propos de la vidéo que tu as mis en lien ici Nossolar (pour à partir de la 18 ième minute)

voilà ce que ça donne en image

  à propos des quatre nombres 153 (Jean21:11) 7 (Apocalypse de Jean 1:20) 144 de 144000  (Apocalypse de Jean 7:4) 666 (Apocalypse de Jean 13:18)

  

Tu as fait une erreur hilbert certainement dut à la fatigue (il est tard ou tôt)!

2 x sinus de 144° = 1.175570505

même en convertissant en radiant ça ne colle pas et c'est normal:
1 radian = 0.174532925
tu aurais du écrire (calcul trouvé sur le net):
2x sin(rad de 54°) = 1.618033989

Dans l'autre post avant le dernier tu dis et en plus c'est juste:
2 x cosinus de 144° = 1.618033989


Là je suis crevé (moi aussi, j'ai pas vérifié le reste) mais j'ai une réflexion (dans le sens à réfléchir ensemble) à te faire et un exemple qui n'y est pas à te donner:
La réflexion:
SOH CAH TOA est la science du triangle et donc du cercle qui devrait être son maximum d'application.
la somme des angles d'un triangle à pour valeur un 1/2 cercle (180°)
Un cercle à la valeur de 2 X la sommes des angles d'un triangle donc 2 x 180° = 360°
Donc le maximum dans le calcul devrait être 360°

Alors pourquoi 666?

Quel rapport avec 360°?

Quel rapport avec 144?

Quel rapport avec Phi et Pi?

Pourquoi ai-je l'impression qu'à des moment avec ces nombres, qu'on nous parle de degré, de surface, de volume, peut être de 4D, "pourquoi mon dieu", au secours hilbertien!

L'exemple qui n'a rien à voir avec la réflexion:

Quand on est curieux qu'on utilise un cosinus puis un sinus et que l'on trouve un nombre remarquable, pourquoi ne pas pousser le vice plus loin avec la tangente juste pour voir le nombre que cela va nous donner?

J'en ri d'avance!



Mais là je suis crevé je te laisse regarder et surtout y bosser.

Mince rassure moi c'est moi qui ne sais plus taper sur ma calculette?
J'ai des trous dans la tête!

Moi je trouve

2 x sinus de 144° = 1.175570505
et
2 x cosinus de 144° = 1.618033989

On est crevé    

c'est exact -2sin (666°) et -2cos(144°)

l'un est un sinus mais l'autre est un cosinus 


je viens de modifier et corriger l'image  
 

Tu as encore la même erreur sur la vignette en dessous de celle où il y a "EXPRIME EN RADIANT"!

C'est pour cela que je te l'ai fait remarqué deux fois!

Mince tu m'as relancé "j'étais en train de regarder un article sur face de bouc où un prof de math tout de miel vêtu à essayer de jouter "poliment" avec notre Gremlins adoré, notre ours national, notre homme des cavernes, un des seuls qui parlent Franc (juste on verra), j'ai nommé le bien nommé monsieur Jacques Grimault.   

Comme il leur parle........ S'il existait pas "j'aimerais qu'on l'invente!"

Allez là j'en peux plus je vais faire la sieste!

Bonne nuit........Euh...."Bonne journée!"

non là c'était ok Christophoros  

il y avait l'erreur que tu as vu -2sin(144°)=PHI alors que c'était plutôt  -2cos(144°)=PHI   mais pas celle là , bon à présent tout est ok 

exprimé en radian on a bien ça 



à plus camarade!

Honnêtement je suis largué dans tout les calculs (et oui hélas, les maths ce n'est pas mon truc...)

Pourtant je dois avoir tord car je remarque bel et bien que tout est mathématique.....

Étrange quand même que ces chiffres "parlent" comme quoi le hasard n'existe pas !

Maintenant petite question si cela fonctionne avec la bible, est-ce que cela fonctionnerai avec d'autre livre sur d'autre religion.....

En tout cas merci au 2 mathématiciens du forum (qui bosse la nuit en plus lol)

Coucou Nosso,  


Moi je ne suis pas matheux, juste quelques notions de base et l'envie hier soir de m'y amuser.

Après oui , toutes les religions travaillent sur "des chiffres" sacré, ne serait-ce d'abord que pour l'astrologie mais pas que....

Hello Cristophoros,

bha tu l'es déjà plus que moi pour avoir vu des petites erreurs chez hilbertien.

Quand on y pense ces livres ont été écrit, puis ré-ecrit et parfois traduit, donc les phrases et surtout les vrais signification on peut-être changées, par contre les chiffres eux reste intactes !!

Je ne sais pas si ils n'ont jamais changé!

Mais dans le doute qu'elle est l'attitude la plus constructive:

1- Balayé la/les théories d'un revers de main de peur de passer pour un incompétent?

2- Ou, chercher vaille que vaille quoiqu'il en coute au risque de perdre sa réputation et son temps?

Bertrand Russell

Les mathématiques, considérées à leur juste mesure, possèdent non seulement la vérité, mais la beauté suprême, une beauté froide et austère, comme celle d'une sculpture, sans référence à une partie de notre fragile nature, sans les effets d'illusion magnifiques de la peinture ou de la musique, pourtant pur et sublime, capable d'une perfection sévère telle que seulement les plus grands arts peuvent la montrer. L'esprit vrai du plaisir, l'exaltation, l'impression d'être plus qu'un homme, qui est la pierre de touche de l'excellence la plus élevée, doit être trouvé dans les mathématiques aussi sûrement que la poésie."

Dans les mathématiques vous êtes  UN HOMME D'EXCEPTION  

si ca peux aider  

Coucou Hilbertien,  

Une question à trois sous, je pense connaître la réponse mais sait-on jamais "mieux vaut être prudent" et donc j'aimerais ton avis:

Imaginons que la terre grandisse, ah mince ça va pas être facile avec ça. Alors prenons la demi-sphère qui comme tous savent maintenant est représenté par la pyramide de Gizeh.
Bon imaginons que la pyramide grossisse tout en gardant ses proportions:
Alors la question c'est: Est-ce-que la valeur de PI ou de PHI en serait faussé comme je l'ai entendu?

Pour moi non! Bien évidemment, mais dans le doute....."la moule" qui me sert de cerveau va peut être apprendre quelque chose de nouveau. Une singularité peut-être?

Merci pour ta réponse

Bonne journée

Rien ne change (N.Or*) sauf la direction du  nord magnétique ( stonehange boussole mais pas que.) et ça vitesse de déplacement.


*Toujours fixe cause loi de l'univers sauf dans un seul cas.

Vue que cette ânerie c'est toi qui l'a dite tes explications + mais pas que ne peuvent être considéré comme une réponse.

Se cacher derrière une posture et penser que tu peux gruger les gens ad vitam æternam est une illusion mais pas que:

La seule personne que tu gruges ici c'est toi même!

 
Ps: Content, pas content.....bonjour, au revoir et merci.

"pas que" veut dire ne souhaite pas partir dans un long débat dont une moule ne comprendrait pas , 
vue que tu me tends la perche ( ça se marie bien avec la moule   )

Ensuite tu n'es pas obligé d'attiser encore un feu de cherche merde.
Si tu sais pas répondre sagement ne le fait pas !
Un conseil tu vas pas faire long feu car l épée est au dessus de ta tête,
et non sur la mienne !