un univers multidimensionnel - la théorie des cordes

une 5ème dimension
L'idée d'un nombre de dimensions supérieur à 4 n'est pas nouvelle. Cette hypothèse a été émise par T. Kaluza, un mathématicien germano-polonais. Ce dernier utilisait une 5ème dimension pour unifier les deux interactions connues à l'époque : l'électromagnétisme développée par J.C. Maxwell, et la gravitation introduite par A. Einstein. La théorie de Kaluza à le mérite de préserver toute la beauté géométrique de la relativité générale, mais y ajoute la lumière en tant que vibration dans la cinquième dimension.

La théorie de Kaluza est améliorée par O.Klein, un physicien suédois. Il parvient à expliquer pourquoi on ne peut pas percevoir cette dimension supplémentaire. Il émet l'hypothèse qu'elle est enroulée sur elle-même telle une feuille dont on ferait un cylindre.

Il suffit alors que ce cylindre ait un rayon extrêmement petit pour devenir imperceptible et se confondre avec une simple ligne, un peu comme un fil de soie très fin ne semble avoir qu’une dimension (la longueur), alors qu’il suffit de le regarder au microscope pour s’assurer qu’il a bien un certain diamètre. Vers 1930, la théorie Kaluza-Klein s'effaça devant la déferlante de la mécanique quantique

la mécanique quantique

E. Schrödinger et W. Heisenberg développent la mécanique quantique, une théorie de l'infiniment petit dans laquelle les particules de matière interagissent entre elles par l'échange de petits paquets d'énergie appelés quanta.
L’électron n’est plus décrit comme une particule à laquelle on peut attribuer une orbite précise.


Le principe d'indétermination montre que l'on peut seulement déterminer avec précision la position ou la vitesse d'une particule mais jamais les deux à la fois. Ce principe se trouve à l'origine du système probabiliste de la mécanique ondulatoire.

la théorie des cordes


Tout ce qui existe dans l' univers serait constitué non pas de particules assimilables à des points comme on le pensait jusqu'à alors mais plutôt à des cordes, sorte de fils ultra minces à une seule dimension...

L'intérêt de la théorie des cordes pour les théoriciens de la physique est qu'elle surmonte, et par là même unifie, les 2 grandes théories de la physique moderne : celle de la "relativité générale" et celle de la "mécanique quantique".

Jusque là, la relativité générale d'Einstein et la mécanique quantique se sont partagées les 4 forces fondamentales auxquelles sont liés tous les phénomènes de la nature.

Ces forces étant la gravitation, l'électromagnétisme, l'interaction faible, et l'interaction forte. Les scientifiques tentèrent alors de combiner ces 4 types d'interactions à l'aide de la théorie dite de la supersymétrie. Mais le problème s'avère néanmoins ardu, les physiciens ne parvenant pas à englober l'interaction gravitationnelle dans leur théorie unificatrice...

la Supersymétrie

Les physiciens rêvent donc d'unifier toutes les interactions existantes en une seule Superforce, laquelle aurait comme propriété une supersymétrie qui unirait les fermions (particules de matière) aux bosons (particules de force).


La supersymétrie transforme la fonction d'onde (représentation mathématique de l'état quantique) d'une particule ordinaire en celle d'une hypothétique superparticule (appelée sparticule) en modifiant la valeur de son spin (rotation de la particule sur elle-même).

Chaque particule va donc être associée à une sparticule correspondant :

Parce que les constituants de la matière sont à la fois des ondes et des particules, le défi que s'est lancé la théorie des cordes est de réconcilier ces deux points de vue... Louis de Broglie précisera à ce sujet que les ondes peuvent justement se comporter comme des particules, et vice versa.

les supercordes vibrent

La théorie des supercordes obéit aux lois de la supersymétrie. Certaines cordes se refermeraient en boucles, d'autres seraient ouvertes et comporteraient donc deux extrémités. Mais leur longueur à toutes seraient des milliards de milliards de fois inférieure à celle d'un noyau d'atome.


A plus grande échelle, elles apparaîtraient comme de simples points et l'on retrouverait alors l'aspect de nos particules "habituelles". Dans la théorie des supercordes, toutes les particules existantes ne seraient en fait que différents modes de vibration d'une seule et unique supercorde...

l'univers selon Calabi-Yau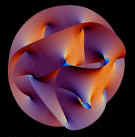
Une classe particulière de formes géométriques six-dimensionnelles satisfait les conditions des équations de la théorie des cordes. Ces figures sont connues sous le nom d'espaces de "Calabi-Yau".
Les calculs montrent que 9 dimensions spatiales indépendantes sont nécessaires à la théorie des cordes. Puisque les cordes sont très petites, non seulement elles peuvent vibrer dans des dimensions grandes et étendues, mais elles peuvent tout aussi bien osciller dans d'autres dimensions, enroulées et minuscules.

Et nous pouvons ainsi satisfaire, dans notre Univers, l'exigence des neuf dimensions spatiales de la théorie des cordes, en supposant qu'en plus de nos trois dimensions spatiales, il en existe six autres enroulées sur elles-mêmes.

Sa théorie représente les particules élémentaires de la physique par des cordes extrêmement petites (100 milliards de milliards de fois plus petites qu'un noyau d'hydrogène) évoluant dans un espace étrange à 10 ou 26 dimensions, pouvant vibrer à différentes fréquences ou "résonances".

Pour décrire les mouvements vibratoires d'une corde, il faut représenter un espace avec un grand nombre de dimensions.
La théorie M" ajoute aux cordes des objets multidimensionnels (les branes) et une dimension spatiale supplémentaire.

Notre Univers serait donc une brane à 5 dimensions (4 pour l'espace-temps celle apportée par la théorie M) auxquelles s'ajoutent les 7 autres dimensions spatiales (très petites) issues de la théorie de supersymétrie.


Dans le cas du scénario de "l'univers Ekpyrotique" proposé en 2001 par Khoury et Steinhardt, le Big Bang correspondrait à une collision entre les branes.

L' Univers serait alors un gaz de "mondes-branes" ne cessant de se croiser et de se percuter générant à chaque fois un nouveau Big Bang...

des Dimensions cachées

Les dimensions supplémentaires seraient si petites qu'a grande échelle nous ne pourrions les détecter. Par exemple, un cheveu semble être un fil à une dimension mais si on l'observe à une échelle de l'ordre de son rayon, il apparaît comme étant un cylindre, donc à deux dimensions.


La théorie affirme que pour détecter une dimension d'échelle D, il faudrait atteindre une énergie de l'ordre de hc/D, où h est la constante de Planck et c, la vitesse de la lumière.

des Dimensions infinies

Notre Univers doit ici être vu comme une brane flottant dans un espace fondamental à 9 dimensions.


Les cordes ouvertes, comme les fermions (quarks) dont est constitué la matière, seraient confinées dans notre brane alors que les cordes fermées comme le graviton pourrait coexister dans d'autres dimensions ce qui expliquerait la faible intensité de la gravitation comparé aux autres forces fondamentales.

documentaire

Ce qu’Einstein ne savait pas encore - Des premières découvertes d’Einstein aux plus récentes théories sur l’interaction des forces, le physicien et mathématicien Brian Greene présente “en toute simplicité” une adaptation télévisée de son best-seller, L’univers élégant.

À l’aide d’images de synthèse éblouissantes et d’expériences simples puisées dans notre quotidien, il explique les différentes étapes de la “théorie des cordes” : une approche révolutionnaire qui pourrait alors expliquer la formation de notre univers.